Pyramid-based Scatterplots Sampling for Progressive and Streaming Data Visualization
Xin Chen, Jian Zhang, Chi-Wing Fu, Jean-Daniel Fekete, Yunhai WangAbstract
We present a pyramid-based scatterplot sampling technique to avoid overplotting and enable progressive and streaming visualization of large data. Our technique is based on a multiresolution pyramid-based decomposition of the underlying density map and makes use of the density values in the pyramid to guide the sampling at each scale for preserving the relative data densities and outliers. We show that our technique is competitive in quality with state-of-the-art methods and runs faster by about an order of magnitude. Also, we have adapted it to deliver progressive and streaming data visualization by processing the data in chunks and updating the scatterplot areas with visible changes in the density map. A quantitative evaluation shows that our approach generates stable and faithful progressive samples that are comparable to the state-of-the-art method in preserving relative densities and superior to it in keeping outliers and stability when switching frames. We present two case studies that demonstrate the effectiveness of our approach for exploring large data.
Results
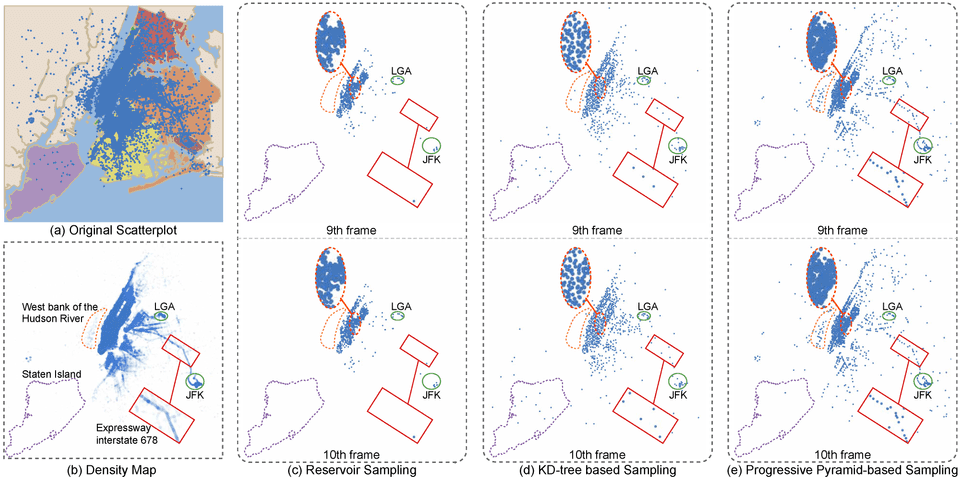
Figure 1: Different sampling methods for presenting the “New York City TLC Trip Record” data with 2 million data points, which are partitioned into chunks, each of 100k data points. (a) The opaque scatterplot is overlaid on the New York map and rendered as (b) a transparent density map, where some major features are highlighted. (c,d,e) The top and bottom rows show the results of different sampling methods in the 9th and 10th frames, respectively, where each result has around 1K points sampled from the original data chunk. Comparing (c) reservoir sampling [28], (d) KD-tree-based sampling [10], and (e) our progressive pyramid-based sampling, we can find our method more consistent in preserving high-density areas (see the LGA and JFK airports circled in green) and low-density areas (see the Expressway interstate 678 labeled by a red rectangle), while maintaining the density difference between different regions (see the Staten Island and the west bank of the Hudson River labeled by the purple and yellow dashed boxes).
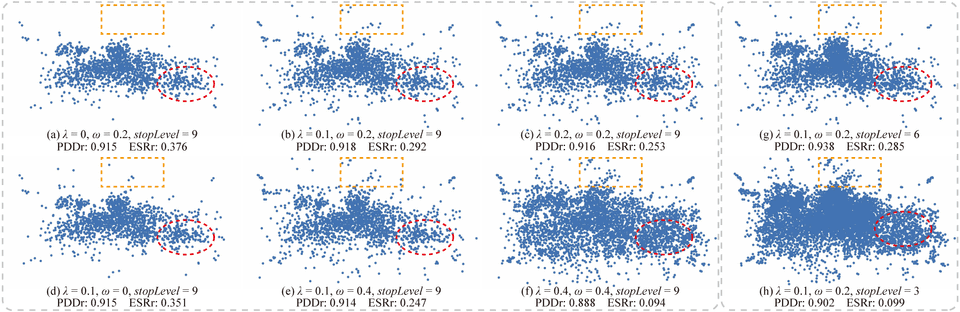
Figure 2: Parameter analysis on the Person Activity dataset [16] with the associated PDDr and ESRr scores (see Section 5). The orange dashed boxes and red dashed circles represent typical low- and medium-density regions, respectively. (a,b,c) A large λ results in more regions classified as low-density regions; (d,b,e) a large ω results in more display samples in low-density regions; (f) when λ and ω are both large, almost all low-density regions in the original scatterplot are kept but the data density ratios cannot be maintained; (b,g,h) decreasing stopLevel introduces more display samples; outliers in low-density regions can be shown more clearly but overplotting will have resulted.
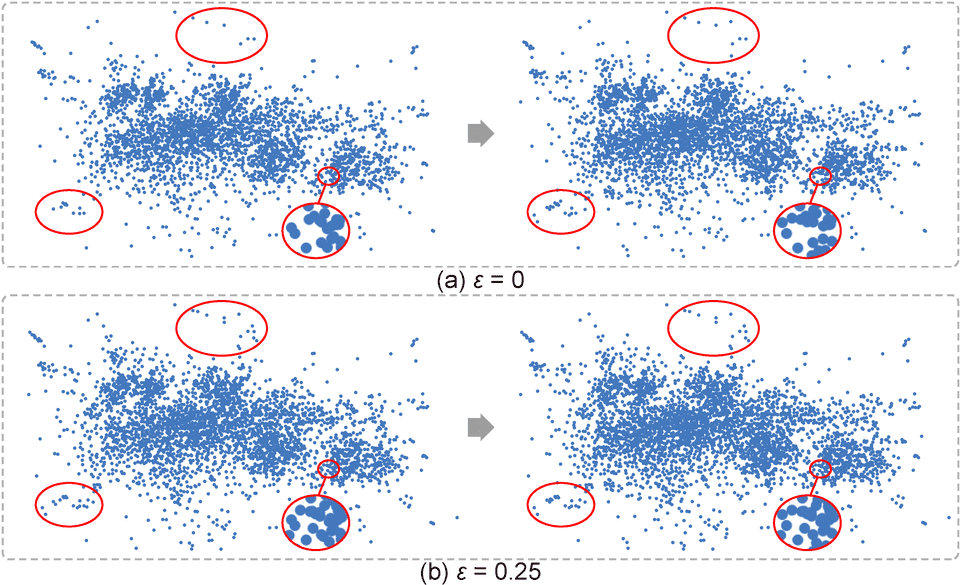
Figure 3: The scatterplots of the 7th and 8th frames under different ε. The red circles show that larger ε can help prevent unnecessary changes of display samples in low-density regions.
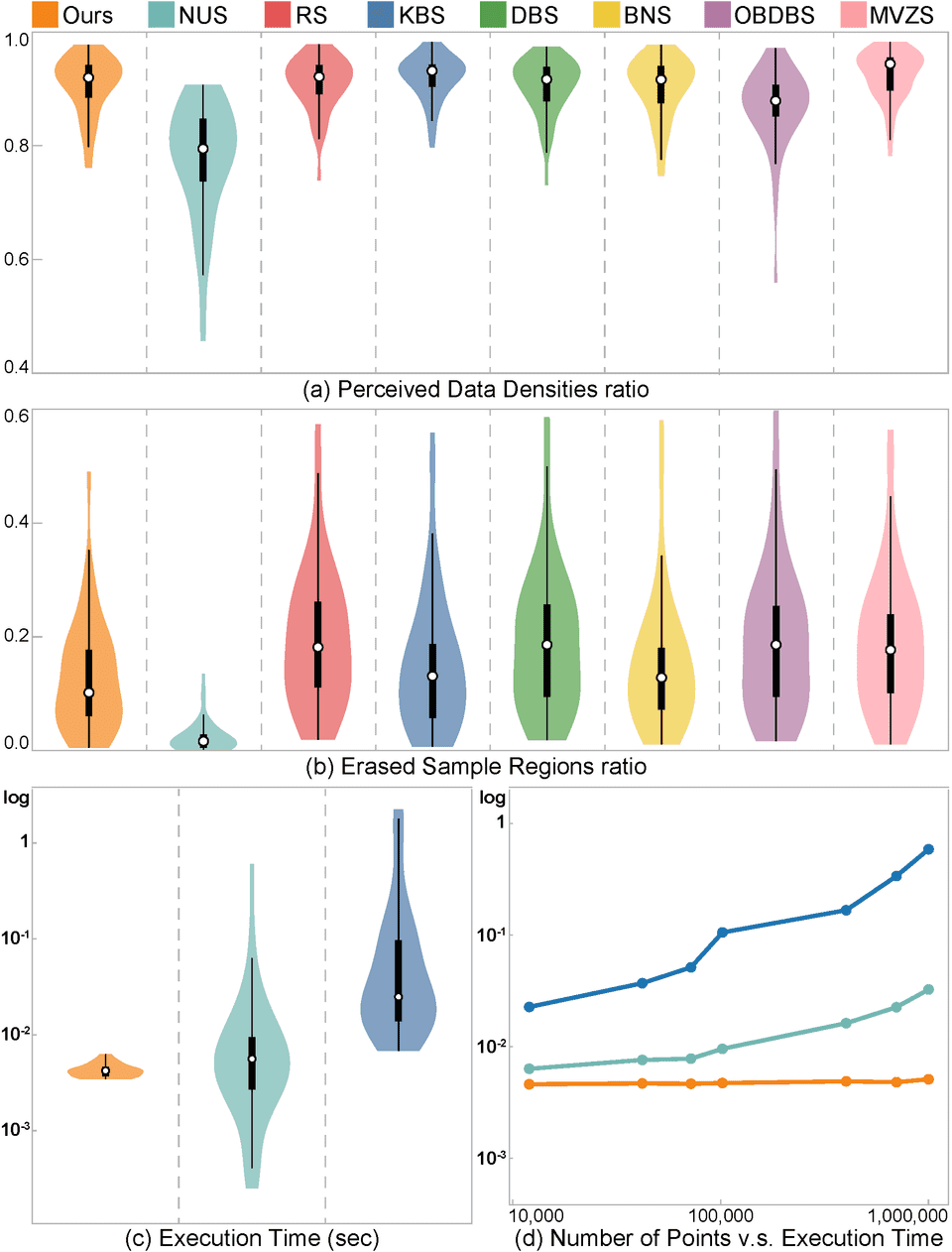
Figure 4: Results of quantitative comparison. (a,b) These violin plots summarize the values of PDDr (a) and ESRr (b) over all the tested datasets, where a larger PDDr score is better and a smaller ESRr score is better; (c) the violin plot shows the log-scale computational times of three most efficient methods with C++ implementations tested over all the datasets; and (d) the curves show the relationship between the execution time (running the sampling procedure) and the data size of different methods by using synthetic datasets.
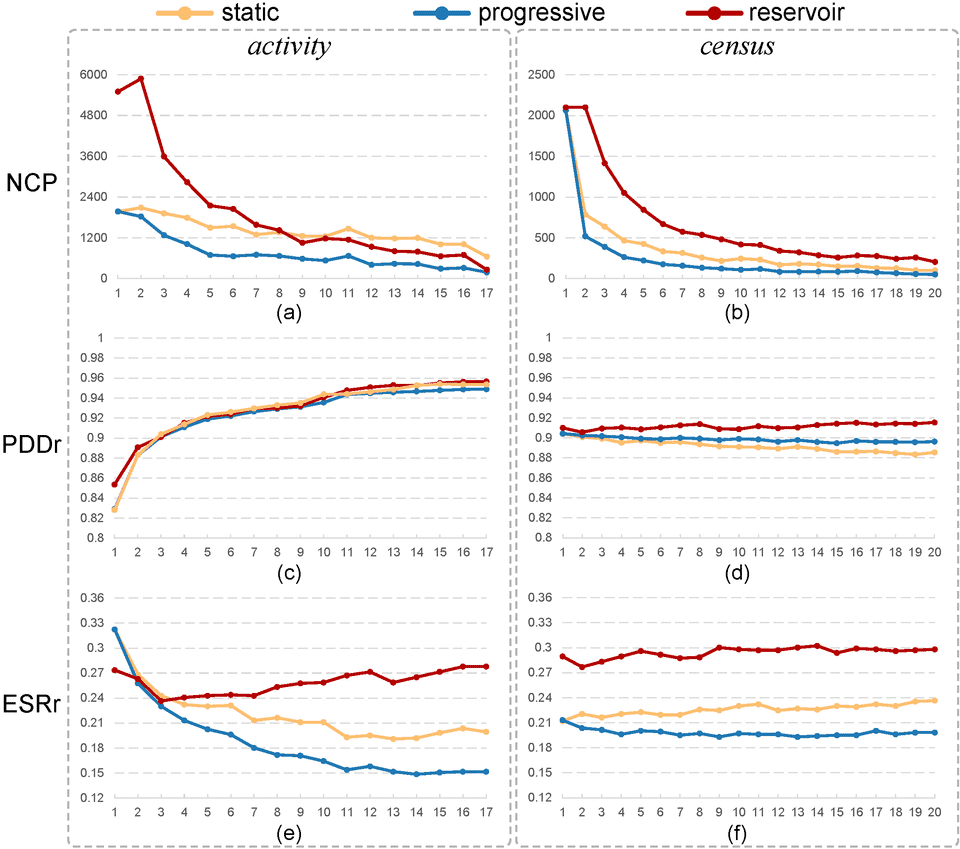
Figure 5: These line charts show how the number of changed points (a,b), PDDr (c,d), and ESRr (e,f) evolve over iterations for loading the two tested datasets (activity and census) for sampling by the three methods being compared: static and progressive versions of our method vs. reservoir sampling. Our progressive method is the most stable and makes a good balance between preserving relative data densities and outliers.
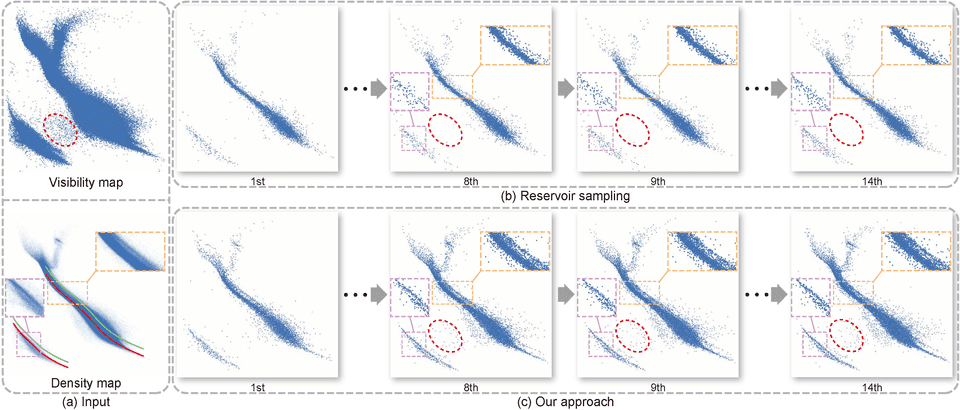
Figure 6: Progressive sampling on the Gaia Data Release 2. (a) the scatterplot of the input data (top) and the density map (bottom); (b,c) the results of the intermediate frames generated by reservoir sampling (b) and our method (c).
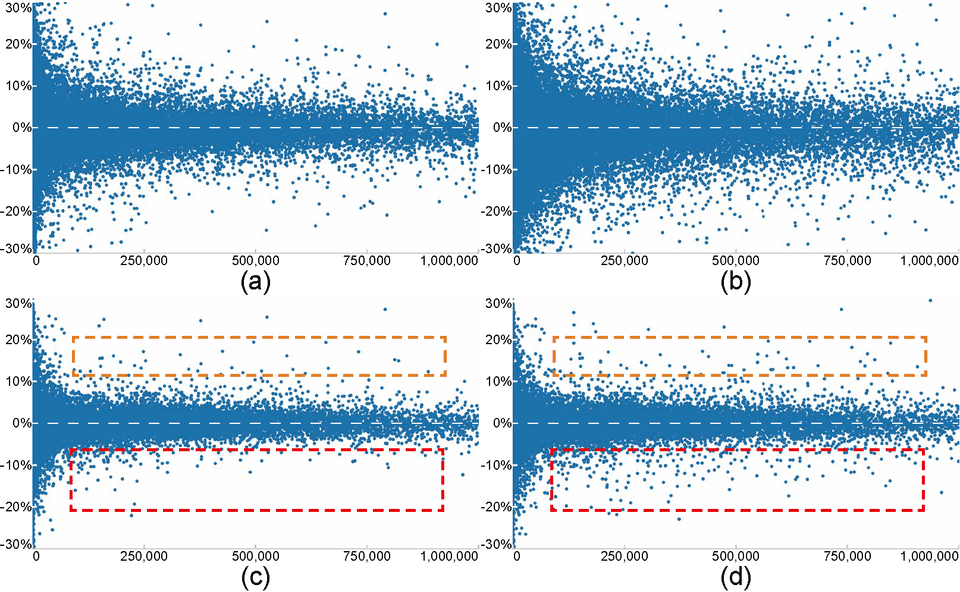
Figure 7: Scatterplots that show the relationship between stock volume (horizontal) and stock percentage change (vertical) for two different time ranges: before the Sep. 11 attacks (left column) and the whole Sep. 2001 (right column). (a,b) the overplotted scatterplots of the original data; and (c,d) streaming visualization results of our method from (a,b), showing that our method can produce faithful visualizations.
Acknowledgements
This work is supported by the grants of the NSFC (61772315, 61861136012), the Open Project Program of State Key Laboratory of Virtual Reality Technology and Systems, Beihang University (No.VRLAB2020C08), and the CAS grant (GJHZ1862).